Восстановление расфокусированных и смазанных изображений

Владимир Южиков


Обработка изображений

Алгоритмы



Восстановление искаженных изображений является одной из наиболее интересных и важных проблем в задачах обработки изображений – как с теоретической, так и с практической точек зрения. Частными случаями являются размытие из-за неправильного фокуса и смаз – эти дефекты, с которым каждый из вас хорошо знаком, очень сложны в исправлении – именно они и выбраны темой статьи. С остальными искажениями (шум, неправильная экспозиция, дисторсия) человечество научилось эффективно бороться, соответствующие инструменты есть в каждом уважающем себя фоторедакторе.




Почему же для устранения смаза и расфокусировки практически ничего нету (unsharp mask не в счет) – может быть это в принципе невозможно? На самом деле возможно – соответствующий математический аппарат начал разрабатываться примерно 70 лет назад, но, как и для многих других алгоритмов обработки изображений, все это нашло широкое применение только в недавнее время. Вот, в качестве демонстрации вау-эффекта, пара картинок:







Я не стал использовать замученную Лену, а нашел свою фотку Венеции. Правое изображение честно получено из левого, причем без использования ухищрений типа 48-битного формата (в этом случае будет 100% восстановление исходного изображения) – слева самый обычный PNG, размытый искусственно. Результат впечатляет… но на практике не все так просто. Под катом подробный обзор теории и практические результаты.

Осторожно, много картинок в формате PNG!

Введение

Начнем издалека. Многие считают, что размытие необратимая операция и информация безвозвратно теряется, т.к. каждый пиксель превращается в пятно, все смешивается, а при большом радиусе размытия так и вовсе получим однородный цвет по всему изображению. Это не совсем так – вся информация просто перераспределяется по некоторому закону и может быть однозначно восстановлена с некоторыми оговорками. Исключение составляет лишь края изображения шириной в радиус размытия – там полноценное восстановление невозможно.



Продемонстрируем это «на пальцах», используя небольшой пример для одномерного случая – представим что у нас есть ряд из пикселей со значениями:

x₁ | x₂ | x₃ | x₄… – Исходное изображение



После искажения значение каждого пикселя суммируется со значением левого, т.е. x’_i = x_i + x_i-1. По идее, надо еще поделить на 2, но опустим это для простоты. В результате имеем размытое изображения со значениями пикселей:

x₁ + x₀ | x₂ + x₁ | x₃ + x₂ | x₄ + x₃… – Размытое изображение



Теперь будем пробовать восстанавливать, вычтем последовательно по цепочке значения по схеме – из второго пиксела первый, из третьего результат второго, из четвертого результат третьего и так далее, получим:

x₁ + x₀ | x₂ — x₀ | x₃ + x₀ | x₄ — x₀… – Восстановленное изображение



В итоге вместо размытого изображения получили исходное изображение, к пикселям которого добавлена неизвестная константа x₀ с чередующимся знаком. Это уже намного лучше – эту константу можно подобрать визуально, можно предположить, что она примерно равна значению x₁, можно автоматически подобрать с таким критерием, чтобы значения соседних пикселей «скакали» как можно меньше и т.д. Но все меняется, как только мы добавляем шум (которые всегда есть в реальных изображениях). При описанной схеме на каждом шаге будет накапливаться вклад шума в общую составляющую, что в итоге может дать совершенно неприемлемый результат, но, как мы убедились, восстановление вполне реально даже таким примитивным способом.

Модель процесса искажения

А теперь перейдем к более формальному и научному описанию этих процессов искажения и восстановления. Будем рассматривать только полутоновые черно-белые изображения в предположении, что для обработки полноцветного изображения достаточно повторить все необходимые шаги для каждого из цветовых каналов RGB. Введем следующие обозначения:

f(x, y) – исходное неискаженное изображение

h(x, y) – искажающая функция

n(x, y) – аддитивный шум

g(x, y) – результат искажения, т.е. то, что мы наблюдаем в результате (смазанное или расфокусированное изображение)



Сформулируем модель процесса искажения следующим образом:

g(x, y) = h(x, y) * f(x, y) + n(x, y) (1)



Задача восстановления искаженного изображения заключается в нахождении наилучшего приближения f'(x, y) исходного изображения. Рассмотрим каждую составляющую более подробно. С f(x, y) и g(x, y) все достаточно понятно. А вот про функцию h(x, y) нужно сказать пару слов – что же она из себя представляет? В процессе искажения каждый пиксель исходного изображения превращается в пятно для случая расфокусировки и в отрезок для случая простого смаза. Либо же можно сказать наоборот, что каждый пиксель искаженного изображения «собирается» из пикселей некоторой окрестности исходного изображения. Все это друг на друга накладывается и в результате мы получаем искаженное изображение. То, по какому закону размазывается или собирается один пиксель и называется функцией искажения. Другие синонимы – PSF (Point spread function, т.е. функция распределения точки), ядро искажающего оператора, kernel и другие. Размерность этой функции, как правило меньше размерности самого изображения – к примеру, в начальном рассмотрении примера «на пальцах» размерность функции была 2, т.к. каждый пиксель складывался из двух.

Искажающие функции

Посмотрим как выглядят типичные искажающие функции. Здесь и далее будем использовать ставший уже стандартным для таких целей инструмент – Matlab, он содержит в себе все необходимое для самых разнообразных экспериментов с обработкой изображений (и не только) и позволяет сосредоточиться на самих алгоритмах, перекладывая всю рутинную работу на библиотеки функций. Впрочем, за это приходится расплачиваться производительностью. Итак, вернемся к PSF, вот примеры их вида:





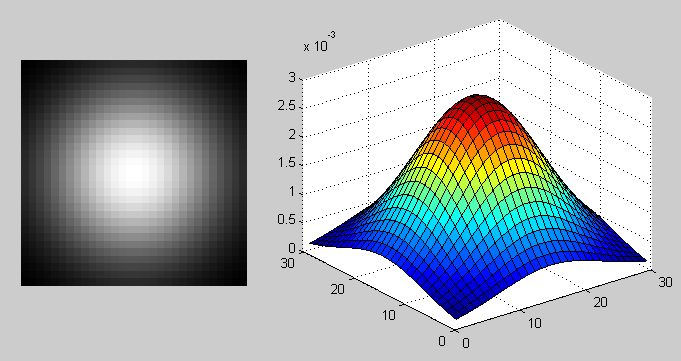PSF в случае размытия по Гауссу функцией fspecial('gaussian', 30, 8);





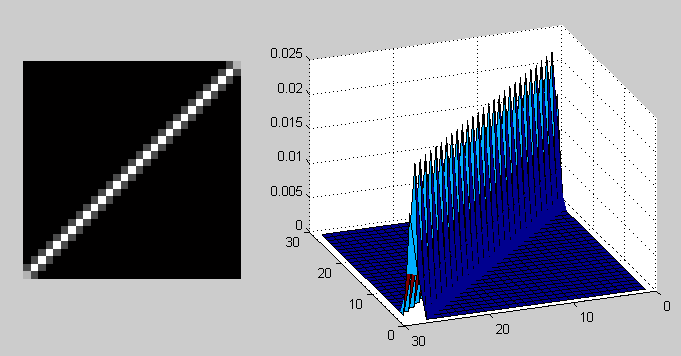PSF в случае смаза фунцией fspecial('motion', 40, 45);



Операция применения искажающей функции к другой функции (к изображению, в данном случае) называется сверткой (convolution), т.е. некоторая область исходного изображения сворачивается в один пиксель искаженного изображения. Обозначается через оператор «*», не путать с обычным умножением! Математически для изображения f с размерами M x N и искажающей функции h c размерами m x n это записывается так:



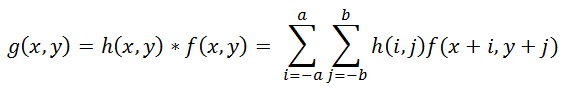
(2)



Где a = (m — 1) / 2, b = (n – 1) / 2. Операция, обратная свертке, называется деконволюцией (deconvolution) и решение такой задачи весьма нетривиально.

Модель шума

Осталось рассмотреть последнее слагаемое, отвечающее за шум, n(x, y) в формуле (1). Причины шума в цифровых сенсорах могут быть самыми разными, но основные это – тепловые колебания и темновые токи. На величину шума также влияет ряд факторов, таких как значение ISO, тип ма трицы, размер пикселя, температура, электромагнитные наводки и пр. В большинстве случаев шум является Гауссовым (который задается двумя параметрами – средним и дисперсией), а также является аддитивным, не коррелирует с изображением и не зависит координат пикселя. Последние три предположения являются очень важными для дальнейшей работы.

Теорема о свертке

Вернемся теперь к первоначальной постановке задачи восстановления – нам необходимо каким-то образом обратить свертку, при этом не забывая про шум. Из формулы (2) видно, что получить f(x, y) из g(x, y) не так-то просто – если решать, что называется, «в лоб», то получится огромная система уравнений. Но на помощь к нам приходит преобразование Фурье, не будем подробно на нем останавливаться, по этой теме уже было сказано немало. Так вот, есть такая теорема о свертке, которая гласит, что операция свертки в пространственной области эквивалентна обычному умножению в частотной области (причем умножение поэлементное, а не матричное). Соответственно, операция обратная свертке эквивалентна делению в частотной области, т.е это можно записать как:

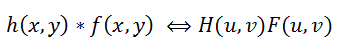
(3)



Где H(u, v), F(u, v) – Фурье-образы соответствующих функций. Значит процесс искажения из формулы (1) можно переписать в частотной области как:

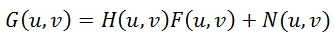
(4)

Инверсная фильтрация

Тут же напрашивается поделить это равенство на H(u, v) и получить следующую оценку F^{^}(u, v) исходного изображения:

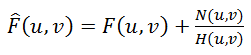
(5)

Это называется инверсной фильтрацией, но на практике практически никогда не работает. Почему же? Чтобы ответить на этот вопрос посмотрим на последнее слагаемое в формуле (5) – если функция H(u, v) принимает значение близкие к нулю или нулевые, то вклад этого слагаемого будет доминирующим. Это практически всегда встречается в реальных примерах – для объяснения этого вспомним как выглядит спектр после преобразование Фурье.

 

Берем исходное изображение,





преобразуем его в полутоновое и, используя Matlab, получаем спектр:

% Load image
I = imread('image_src.png');
figure(1); imshow(I); title('Исходное изображение'); 
% Convert image into grayscale
I = rgb2gray(I);
% Compute Fourier Transform and center it
fftRes = fftshift(fft2(I));
% Show result
figure(2); imshow(mat2gray(log(1+abs(fftRes)))); title('FFT - Амплитудный спектр (логарифмическая шкала)');
figure(3); imshow(mat2gray(angle(fftRes))); title('FFT - Фазовый спектр');

В результате получаем две компоненты: амплитудный и фазовый спектры. Про фазу, кстати, многие забывают. Обратите внимание, что амплитудный спектр показан в логарифмической шкале, т.к. его значения варьируются очень сильно – на несколько порядков, в центре максимальные значения (порядка миллионов) и быстро убывают практически до нулевых по мере удаления от центра. Именно из-за этого инверсная фильтрация будет работать только при нулевых или практически нулевых значениях шума. Продемонстрируем это на практике с помощью следующего скрипта:

% Load image
I = im2double(imread('image_src.png')); 
figure(1); imshow(I); title('Исходное изображение');
% Blur image
Blurred = imfilter(I, PSF,'circular','conv' );
figure(2); imshow(Blurred); title('Размытое изображение');
% Add noise
noise_mean = 0;
noise_var = 0.0;
Blurred = imnoise(Blurred, 'gaussian', noise_mean, noise_var);
% Deconvolution
figure(3); imshow(deconvwnr(Blurred, PSF, 0)); title('Результат');

          noise_var = 0.0000001                            noise_var = 0.000005

Хорошо видно, что добавление даже очень небольшого шума приводит к значительным помехам, что сильно ограничивает практическое применение метода.

Существующие подходы для деконволюции

Но есть подходы, которые учитывают учитывают наличие шума на изображении – один из самых известных и самых первых, это фильтр Винера (Wiener). Он рассматривает изображение и шум как случайные процессы и находит такую оценку f' для неискаженного изображения f, чтобы среднеквадратическое отклонение этих величин было минимальным. Минимум этого отклонения достигается на функции в частотной области:

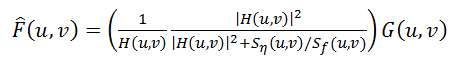
(6)

Этот результат был получине Винером в 1942 году. Подробный вывод здесь приводить не будем, те, кто интересуется, могут посмотреть его здесь . Функцией S здесь обозначаются энергетические спектры шума и исходного изображения соответственно – поскольку, эти величины редко бывают известны, то дробь S_n / S_f заменяют на некоторую константу K, которую можно приблизительно охарактеризовать как соотношение сигнал-шум.



Следующий метод, это «сглаживающая фильтрация методом наименьших квадратов со связью», другие названия: «фильтрация по Тихонову», «Тихоновская регуляризация». Его идея заключается в формулировке задачи в матричном виде с дальнейшем решением соответствующей задачи оптимизации. Это решение записывается в виде:

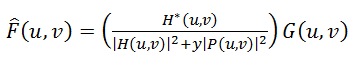
(7)

Где y – параметр регуляризации, а P(u, v) – Фурье-преобразование оператора Лапласа (матрицы 3 * 3).



Еще один интересный подход предложили независимо Ричардосн [Richardson, 1972] и Люси [Lucy, 1974]. Метод так и называется «метод Люси-Ричардсона». Его отличительная особенность в том, что он является нелинейным, в отличие от первых трех – что потенциально может дать лучший результат. Вторая особенность – метод является итерационным, соответственно возникают трудности с критерием останова итераций. Основная идея состоит в использовании метода максимального правдоподобия для которого предполагается, что изображение подчиняется распределению Пуассона. Формулы для вычисления достаточно простые, без использования преобразования Фурье – все делается в пространственной области:

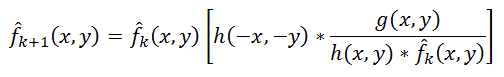
(8)

Здесь символом «*», как и раньше, обозначается операция свертки. Этот метод широко используется в программах для обработки астрономических фотографий – в них использование деконволюции (вместо unsharp mask, как в фоторедакторах) является стандартом де-факто. В качестве примера можно привести Astra Image, вот примеры деконволюции. Вычислительная сложность метода очень большая – обработка средней фотографии, в зависимости от количества итераций, может знанимать многие часы и даже дни.



Последний рассматриваемый метод, а вернее, целое семейство методов, которые сейчас активно разрабатываются и развиваются – это слепая деконволюция (blind deconvolution). Во всех предыдущих методах предполагалось, что искажающая функция PSF точно известна, в реальности это не так, обычно PSF известна лишь приблизительно по характеру видимых искажений. Слепая деконволюция как раз является попыткой учитывать это. Принцип достаточно простой, если не углубляться в детали – выбирается первое приближение PSF, далее по одному из методов делается деконволюция, после чего некоторым критерием определяется степень качества, на осн ове нее уточняется функция PSF и итерация повторяется до достижения нужного результата.

Практика

Теперь с теорией все – перейдем к практике, начнем со сравнения перечисленных методов на изображении с искусственным размытием и шумом.

% Load image
I = im2double(imread('image_src.png'));
figure(1); imshow(I); title('Исходное изображение');

% Blur image
PSF = fspecial('disk', 15);
Blurred = imfilter(I, PSF,'circular','conv' );

% Add noise
noise_mean = 0;
noise_var = 0.00001;
Blurred = imnoise(Blurred, 'gaussian', noise_mean, noise_var);
figure(2); imshow(Blurred); title('Размытое изображение');
estimated_nsr = noise_var / var(Blurred(:));

% Restore image
figure(3), imshow(deconvwnr(Blurred, PSF, estimated_nsr)), title('Wiener');
figure(4); imshow(deconvreg(Blurred, PSF)); title('Regul');
figure(5); imshow(deconvblind(Blurred, PSF, 100)); title('Blind');
figure(6); imshow(deconvlucy(Blurred, PSF, 100)); title('Lucy');

Результаты:





Фильтр Винера





Регуляризация по Тихонову





Фильтр Люси-Ричардсона





Слепая деконволюция

Заключение

И в конце первой части немного затронем примеры реальных изображений. До этого все искажения были искусственными, что конечно хорошо для обкатки и изучения, но очень интересно посмотреть, как все это будет работать с настоящими фотографиями. Вот один пример такого изображения, снятого зеркалкой Canon 500D с ручным уводом фокуса:







Далее запускаем несложный скрипт:

% Load image
I = im2double(imread('IMG_REAL.PNG'));
figure(1); imshow(I); title('Исходное изображение');

%PSF
PSF = fspecial('disk', 8);
noise_mean = 0;
noise_var = 0.0001;
estimated_nsr = noise_var / var(I(:));

I = edgetaper(I, PSF);
figure(2); imshow(deconvwnr(I, PSF, estimated_nsr)); title('Результат');

И получаем следующий результат:







Как видно, на изображении появились новые детали, четкость стала гораздо выше, правда появились и помехи в виде «звона» на контрастных границах.



И пример с реальным смазом — для его осуществления фотоаппарат был установлен на штатив, выставлена относительно длинная выдержка и равномерным движением в момент срабатывания затвора был получен смаз:





Скрипт примерно тот же, только тип PSF теперь «motion»:

% Load image
I = im2double(imread('IMG_REAL_motion_blur.PNG'));
figure(1); imshow(I); title('Исходное изображение');

%PSF
PSF = fspecial('motion', 14, 0);
noise_mean = 0;
noise_var = 0.0001;
estimated_nsr = noise_var / var(I(:));

I = edgetaper(I, PSF);
figure(2); imshow(deconvwnr(I, PSF, estimated_nsr)); title('Результат');

Результат:





Качество, опять же, заметно улучшилось — стали различимы рамы на окнах, машины. Артефакты уже другие, нежели в предыдушем примере с расфокусировкой.



На этом интересном и закончим первую часть.

Во второй части я сосредоточусь на проблемах обработки реальных изображений — построения PSF и их оценки, рассмотрю более сложные и продвинутые техники деконволюции, методы устранения дефектов типа звона, проведу обзор и сравнения существующего ПО и прочее.



P.S. Не так давно была опубликована статья на хабре про Исправление смазанных фотографий в новой версии Photoshop

Для тех, кто хочет поиграться с похожей технологией устранения смаза (возможно, той самой, что будет использоваться в фотошопе), можно по этой ссылке скачать демо-версию приложения, посмотреть примеры восстановления, а также почитать про принцип работы.

Литература

Гонсалес Р., Вудс Р. Цифровая обработка изображений

Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB

Восстановление расфокусированных и смазанных изображений. Практика

Не так давно я опубликовал на хабре первую часть статьи по восстановлению расфокусированных и смазанных изображений, где описывалась теоретическая часть. Эта тема, судя по комментариям, вызвала немало интереса и я решил продолжить это направление и показать вам какие же проблемы появляются при практической реализации казалось бы простых формул.

В дополнение к этому я написал демонстрационную программу, в которой реализованы основные алгоритмы по устранению расфокусировки и смаза. Программа выложена на GitHub вместе с исходниками и дистрибутивами.

Ниже показан результат обработки реального размытого изображения (не с синтетическим размытием). Исходное изображение было получено камерой Canon 500D с объективом EF 85mm/1.8. Фокусировка была выставлена вручную, чтобы получить размытие. Как видно, текст совершенно не читается, лишь угадывается диалоговое окно Windows 7.



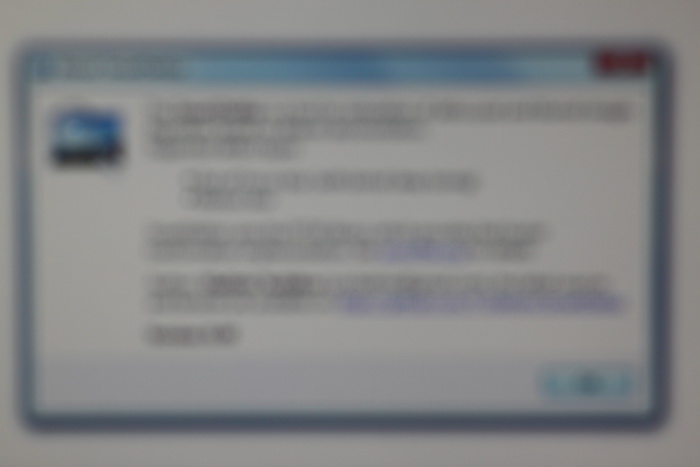
И вот результат обработки:



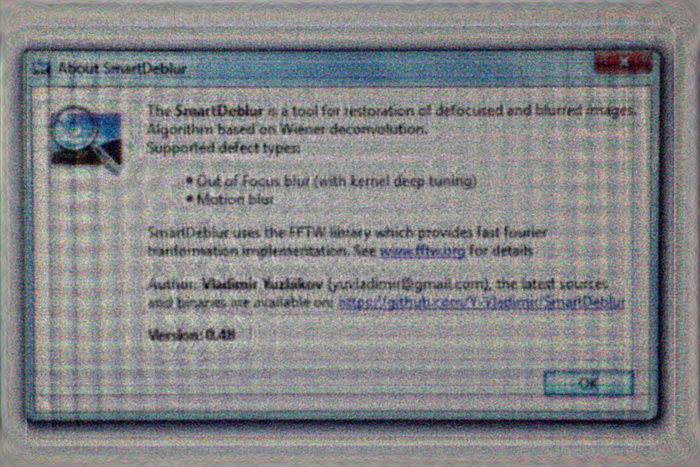
Практически весь текст читается достаточно хорошо, хотя и появились некоторые характерные искажения.

Под катом подробное описание проблем деконволюции, способов их решения, а также множество примеров и сравнений. Осторожно, много картинок!

Вспомним теорию

Подробное описание теории было в первой части, но все же напомню вкратце основные моменты. В процессе искажения из каждого пикселя исходного изображения получается некоторое пятно в случае расфокусировки и отрезок для случая обычного смаза. Все это друг на друга накладывается и в результате мы получаем искаженное изображение — это называется сверткой изображения или конволюцией. То, по какому закону размазывается один пиксель и называется функцией искажения. Другие синонимы – PSF (Point spread function, т.е. функция распределения точки), ядро искажающего оператора, kernel и другие.



Чтобы восстановить исходное изображение нам необходимо каким-то образом обратить свертку, при этом не забывая про шум. Но это не так-то просто – если действовать, что называется, «в лоб», то получится огромная система уравнений, которую решить за приемлемое время невозможно.

Но на помощь к нам приходит преобразование Фурье и теорема о свертке, которая гласит, что операция свертки в пространственной области эквивалентна обычному умножению в частотной области (причем умножение поэлементное, а не матричное). Соответственно, операция обратная свертке эквивалентна делению в частотной области. Поэтому процесс искажения можно переписать следующим образом:

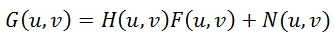
(1),

где все элементы — это фурье-образы соответствующих функций:

G(u,v) – резуль тат искажения, т.е. то, что мы наблюдаем в результате (смазанное или расфокусированное изображение)

H(u,v) – искажающая функция, PSF

F(u,v) – исходное неискаженное изображение

N(u,v) – аддитивный шум



Итак, нам нужно восстановить максимальное приближение к исходному изображению F(u,v). Просто поделить правую и левую часть на H(u,v) не получится, т.к. при наличии даже совсем небольшого шума (а он всегда есть на реальных изображениях) слагаемое N(u,v)/H(u,v), будет доминировать, что приведет к тому, что исходное изображение будет целиком скрыто под шумом.



Чтобы решить эту проблему, были разработаны более устойчивые методы, одним из которых являтся фильтр Винера (Wiener). Он рассматривает изображение и шум как случайные процессы и находит такую оценку f' для неискаженного изображения f, чтобы среднеквадратическое отклонение этих величин было минимальным:

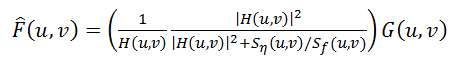
(2)

Функцией S здесь обозначаются энергетические спектры шума и исходного изображения соответственно – поскольку, эти величины редко бывают известны, то дробь S_n / S_f заменяют на некоторую константу K, которую можно приблизительно охарактеризовать как соотношение сигнал-шум.

Способы получения PSF

Итак, возьмем за отправную точки описанный фильтр Винера — вообще говоря, существует множество других подходов, но все они дают примерно одинаковые результаты. Так что все описанное ниже будет справедливо и для остальных методов деконволюции.



Основная задача — получить оценку функции распределения точки (PSF). Это можно сделать несколькими способами:

1. Моделирование. Очень непросто и трудоемко, т.к. современные объективы состоят из десятка, другого различных линз и оптических элементов, часть из которых имеет асферическую форму, каждый сорт стекла имеет свои уникальные характеристики преломления лучей с той или иной длиной волны. В итоге задача корректного расчета распространение света в такой сложнейшей оптической системе с учетом влияния диафрагмы, переотражений и т.п. становится практически невозможной. И решение ее, пожалуй, доступно только разработчикам современных объективов.

2. Непосредственное наблюдение. Вспомним, что PSF — это то, во что превращается каждая точка изображения. Т.е. если мы сформируем черный фон и одну белую точку на нем, а затем сфотографируем это с нужным значением расфокусировки, то мы получим непосредственно вид PSF. Кажется просто, но есть много нюансов и тонкостей.

3. Вычисление или косвенное наблюдение. Присмотримся к формуле (1) процесса искажение и подумаем, как можно получить H(u,v)? Решение приходит сразу — нужно иметь исходное F(u,v) и искаженное G(u,v) изображения. Тогда поделив фурье-образ искаженного изображения на фурье-образ исходного изображения мы получим искомую PSF.

Про боке

Перед тем как перейдем к деталям, расскажу немного теории расфокусировки применительно к оптике. Идеальный объектив имеет PSF в виде круга, соответственно каждая точка превращается в круг некоторого диаметра. Кстати, это для многих неожиданность, т.к. с первого взгляда кажется, что дефокус просто растушевывает все изображение. Это же объясняет и то, почему фотошоповское размытие Гаусса совсем не похоже на тот рисунок фона (его еще называют боке), который мы видим у объективов. На самом деле это два разных типа размытия — по Гауссу каждая точка превращается в нечеткое пятно (колокол Гаусса), а дефокус каждую точку превращает в круг. Соответственно и разные результаты.



Но идеальных объективов у нас нет и в реальности мы получаем то или иное отклонение от идеального круга. Именно это и формирует неповторимый рисунок боке каждого объектива, заставляя фотографов тратить кучу денег на объективы с красивым боке :) Боке можно условно разделить на три типа:

— Нейтральное. Это максимальное приближение к кругу

— Мягкое. Когда края имеют меньшую яркость, чем центр

— Жесткое. Когда края имеют большую яркость, чем центр.



Рисунок ниже иллюстрирует это:





Более того, тип боке — мягкое или жесткое зависит еще и от того, передний это фокус или задний. Т.е. фотоаппарат сфокусирован перед объектом или же за ним. К примеру, если объектив имеет мягкий рисунок боке в переднем фокусе (когда, скажем, фокус на лице, а задний план размыт), то в заднем фокусе боке того же объектива будет жестким. И наоборот. Только нейтральное боке не меняется от вида фокуса.



Но и это еще не все — поскольку каждому объективу присущи те или иные геометрические искажения, то вид PSF зависит еще и от положения. В центре — близко к кругу, по краям — эллипсы и другие сплюснутые фигуры. Это хорошо видно на следующем фото — обратите внимание на правый нижний угол:





А теперь рассмотрим подробнее два последних метода получения PSF.

PSF — Непосредственное наблюдение

Как уже говорилось выше, необходимо сформировать черный фон и белую точку. Но просто напечатать на принтере одну точку недостаточно. Необходим намного большее отличие в яркости черного фона и белой точки, т.к. одна точка будет размываться по большому кругу — соответственно должна иметь большую яркость, чтобы быть видной после размытия.



Для этого я распечатал черный квадрат Малевича (да, тонера много ушло, но чего не сделаешь ради науки!), наложил с другой стороны фольгу, т.к. лист бумаги все же неплохо просвечивает и иголкой проколол маленькую дырочку. Затем соорудил нехитрую конструкцию из 200-ваттной лампы и сэндвича из черного листа и фольги. Выглядело это вот так:





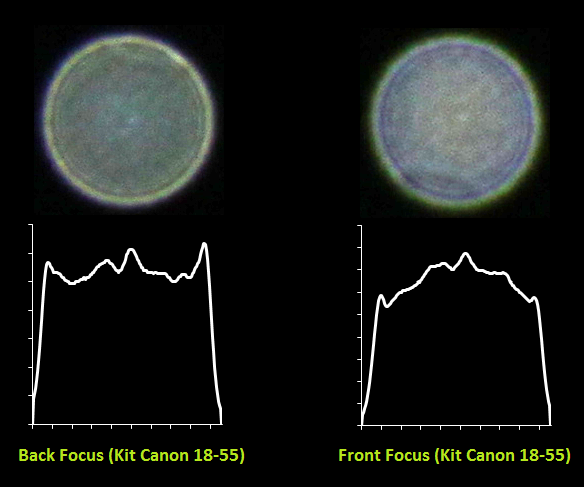
Далее включил лампу, закрыл ее листом, выключил общий свет и сделал несколько фоток используя два объектива — китовый Canon EF 18-55 и портретник Canon EF 85mm/1.8. Из получившихся фоток я вырезал PSF и затем построил графики профилей.

Вот что получилось для китового объектива:





И для портретника Canon EF 85mm/1.8:





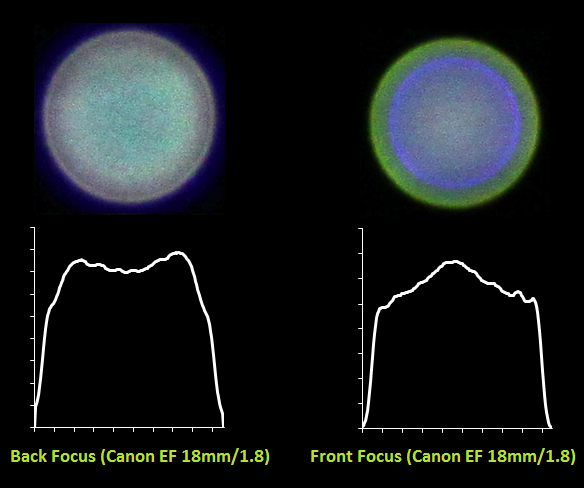
Хорошо видно как меняется характер боке с жествкого на мягкий для одного и того же объектива в случае переднего и заднего фокуса. Также видно, какую непростую форму имеет PSF — она весьма далека от идеального круга. Для портретника также видны большие хроматические аберрации из-за большой светосилы объектива и малой диафрагмы 1.8.

И вот еще пара снимков при диафрагме 14 — на нем видно, как поменялась форма с круга на правильный шестиугольник:

PSF — Вычисление или косвенное наблюдение

Следующий подход — косвенное наблюдение. Для этого, как писалось выше, нам нужно иметь исходное F(u,v) и искаженное G(u,v) изображения. Как их получить? Очень просто — необходимо поставить фотоаппарат на штатив и сделать один резкий и один размытый снимок одного и того изображения. Далее с помощью деления фурье-образа искаженного изображения на фурье-образ исходного изображения мы получим фурье-образ нашей искомой PSF. После чего применив обратное преобразование Фурье получим PSF в прямом виде.

Я сделал два снимка:









И в результате получил во т такую PSF:

На горизонтальную линию не обращайте внимания, это артефакт после преобразования Фурье в матлабе. Результат, скажем так, средненький — очень много шумов и детали PSF видны не так хорошо. Тем не менее, метод имеет право на существование.

Описанные методы можно и нужно использовать для построения PSF при восстановлении размытых изображений. Т.к. от того, насколько эта функция приближена к реальной напрямую зависит качество восстановления исходного изображения. При несовпадении предполагаемой и реальной PSF будут наблюдаться многочисленные артефакты в виде «звона», ореолов и снижения четкости. В большинстве случаев предполагается форма PSF в виде круга, тем не менее для достижения максимальной степени восстановления рекомендуется поиграться с формой этой функции, попробовав несколько вариантов от распространенных объективов — как мы видели, форма PSF может варьироваться в значительной степени в зависимости от диафрагмы, объектива и прочих условий.

Краевые эффекты

Следующая проблема заключается в том, что если напрямую применить фильтр Винера, то на краях изображения будет своеобразный «звон». Его причина, если объяснять на пальцах, заключается в следующем — когда делается деконволюция для тех точек, которые расположены на краях, то при сборке не хватает пикселей, которые находятся за краями изображения и они принимаются либо равным нулю, либо берутся с противоположной стороны (зависит от реализации фильтра Винера и преобразования Фурье). Выглядит это так:


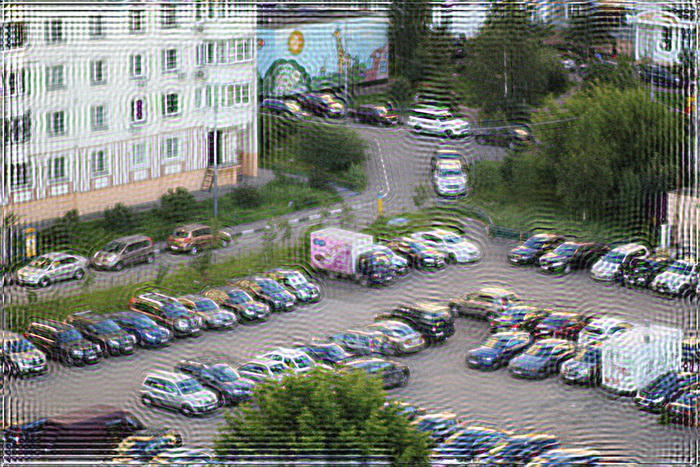
Одно из решений, чтобы избежать этого состоит предобработке краев изображения. Они размываются с помощью той же самой PSF. На практике это реализуется следующем образом — берется входное изображение F(x,y), размывается с помощью PSF и получается F'(x,y), затем итоговое входное изображение F''(x,y) формируется суммированием F(x,y) и F'(x,y) с использованием весовой функции, которая на краях принимает значение 1 (точка целиком берется из размытого F'(x,y)), а на расстоянии равном (или большем) радиусу PSF от края изображения принимает значение 0. Результат получается такой — звон на краях исчез:

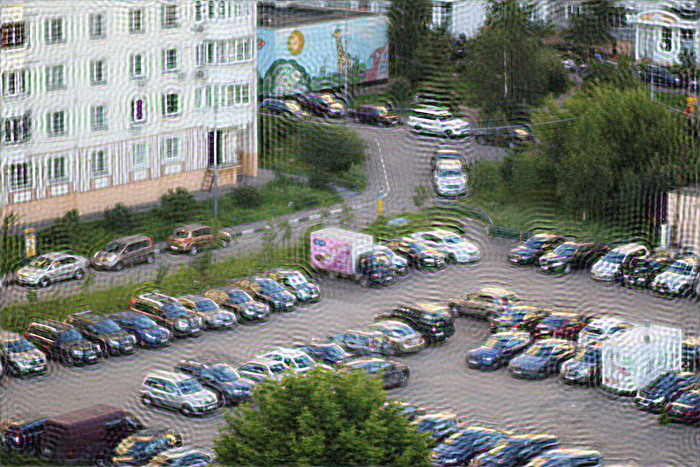
Практическая реализация

Я сделал программу, демонстрирующую восстановление смазанных и расфокусированных изображений. Написана она на C++ с использованием Qt. В качестве реализации преобразования Фурье я выбрал библиотеку FFTW, как самую быструю из опен-соурсных реализаций. Называется моя программа SmartDeblur, скачать ее можно на странице github.com/Y-Vladimir/SmartDeblur, все исходники открыты под лицензией GPL v3.
Скриншот главного окна:


Основные функции:
— Высокая скорость. Обработка изображения размером 2048*1500 пикселей занимает около 300мс в режиме Preview (когда перемещаются ползунки настроек) и 1.5 секунды в чистовом режиме (когда отпустили ползунки настроек).
— Подбор параметров в Real-time режиме. Нет необходимости нажимать кнопки Preview, все делается автоматически, нужно лишь двигать ползунки настроек искажения
— Вся обработка идет для изображения в полном разрешении. Т.е. нет никакого маленького окошка предпросмотра и кнопок Apply.
— Поддержка восстановления смазанных и расфокусированных изображений
— Возможность подстройки вида PSF

Основной упор при разработке был сделан на скорость. В итоге она получилась такая, что превосходит коммерческие аналоги в десятки раз. Вся обработка сделана по-взрослому, в отдельном потоке. За 300 мс программа успевает сгенерить новую PSF, сделать 3 преобразования Фурье, сделать деконволюцию по Винеру и отобразить результат — и все это для изображения размером 2048*1500 пикселей. В чистовом режиме делается 12 преобразований Фурье (3 для каждого канала, плюс одно для каждого канала для подавления краевых эффектов) — это занимает около 1.5 секунд. Все времена указаны для процессора Core i7.

Пока в программе есть ряд багов и особенностей — скажем, при некоторых значениях настроек изображение покрывается рябью. Точно причину выяснить не удалось, но предположительно — особенности работы библиотеки FFTW.
Ну и в целом в процессе разработки пришлось обходить множество скрытых проблем как в FFTW (например не поддерживаются изображения с нечетным размером одной из сторон, типа 423*440.). Были проблемы и с Qt — выяснилось, что рендеринг линии со включенным Antialiasing работает не совсем точно. При некоторых значениях углов линия перескакивала на доли пикселя, что давало артефакты в виде сильной ряби. Для обхода этой проблемы добавил строчки:

    // Workarround to have high accuracy, otherwise drawLine method has some micro-mistakes in the rendering    QPen pen = kernelPainter.pen();    pen.setWidthF(1.01);    kernelPainter.setPen(pen);

Сравнение

Осталось сравнить качество обработки с коммерческими аналогами.
Я выбрал 2 самые известные программы
1. Topaz InFocus — www.topazlabs.com/infocus/
2. Focus Magic — www.focusmagic.com/

Для чистоты эксперимента будем брать те рекламные изображения, которые приведены на официальных сайтах — так гарантируется, что параметры тех программ выбраны оптимальными (т.к. думаю, разработчики тщательно отбирали изображения и подбирали параметры перед публикацией в рекламе на сайте).
Итак поехали — восстановление смаза:
Берем пример с сайта Topaz InFocus www.topazlabs.com/infocus/_images/licenseplate_compare.jpg

Обрабатываем с вот такими параметрами:

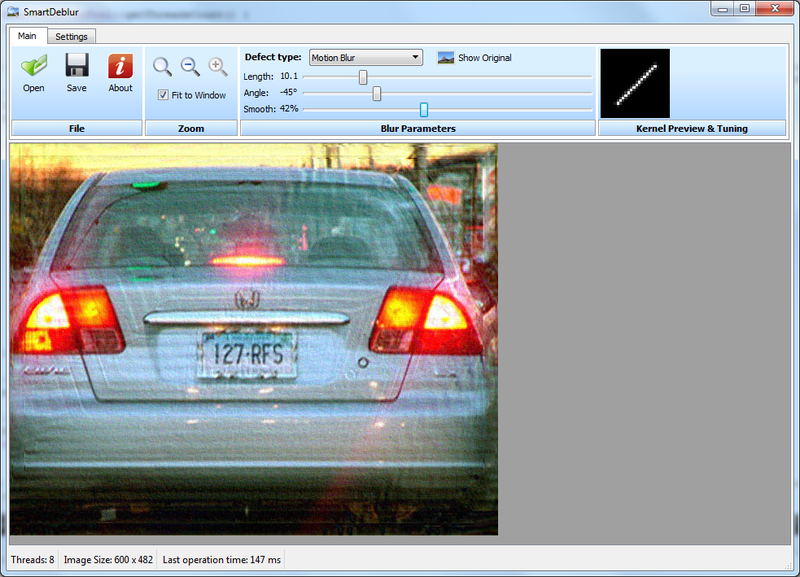
и получаем такой результат:

Результат с сайта Topaz InFocus:


Результат весьма схожий, это говорит о том, что в основе Topaz InFocus используется похожий алгоритм деконволюции плюс постобработка в виде заглаживания-удаления шумов и подчеркивания контуров.
Примеров сильно дефокусировки на сайте этой программы найти не удалось, да и она не предназначена для этого (максимальный радиус размытия составляет всего несколько пикселей).
Можно отметить еще один момент — угол наклона оказался ровно 45 градусов, а длина смаза 10 пикселей. Это наводит на мысль о том, что изображение смазано искусственно. В пользу этого факта говорит и то, что качество восстановления очень хорошее.

Пример номер два — восстановление дефокусировки. Для этого возьмем пример с сайта Focus Magic: www.focusmagic.com/focusing-examples.htm

Получили вот такой результат:

Результат SmartDeblur	Результат Focus Magic

Тут уже не так очевидно, что лучше.

Заключение

На этом я хотел бы закончить эту статью. Хотя и много чего еще хотелось написать, но и так уже длинн ый текст получился. Буду очень признателен, если попробуете скачать SmartDeblur и потестировать на реальных изображениях — у меня, к сожалению, не так много расфокусированных и смазанных изображений, все поудалял :)

И буду особо признателен, если пришлете мне (мыло есть в профиле) свой фидбек и примеры удачных/неудачных восстановлений. Ну и просьба сообщать о всех багах, замечаниях, предложениях — т.к. приложение еще пока местами сыроватое и немного нестабильное.

P.S. Исходники пока не очень чистые в плане стиля — там пока куча утечек памяти, еще не успел перевести на смарт-поинтеры, поэтому после нескольких изображений может перестать открывать файлы. Но в целом работает :)

Восстановление расфокусированных и смазанных изображений. Повышаем качество

Представляю вашему вниманию заключительную статью из трилогии «Восстановление расфокусированных и смазанных изображений». Первые две вызвали заметный интерес — область, действительно, интересная. В этой части я рассмотрю семейство методов, которые дают лучшее качество, по сравнении со стандартным Винеровским фильтром — это методы, основанные на Total Variaton prior.

Также по традиции я выложил новую версию SmartDeblur (вместе с исходниками в open-source) в которой реализовал этот метод. Итоговое качество получилось на уровне коммерческих аналогов типа Topaz InFocus. Вот пример обработки реального изображения с очень большим размытием:

Введение

Описывать базовую теорию деконволюции здесь я не буду, о ней очень подробно было написано в предыдущих статьях. Тем, кто не читал их или подзабыл, рекомендую для начала ознакомиться с ними, чтобы понять терминологию и классические подходы:



Часть 1. Теория;

Часть 2. Практика.



Прежде чем перейти к описанию Total Variation (далее TV prior), необходимо понять, какие же недостатки есть у алгоритмов типа классического Винеровского фильтра? Самые основные — это эффект типа звона (периодический ореол на краях объектов) даже при небольшом уровне шума, размывание границ и мелких деталей, а также плохое шумоподавление с точки зрения человеческого восприятия. Все это сильно мешает практическому применению фильтра Винера ограничивая его применение задачами технического восстановления изображений, например для прочтения интересующих надписей.

Поэтому в последнее время было разработано большое количество самых разных методов, цель которых состоит в улучшении визуального качества. Надо заметить, что количество деталей при этом, как правило не возрастает.

Описание TV prior

Основное качество Total Variation prior с точки зрения результата — сохранение резких краев и сглаживание артефактов деконволюции. Записывается следующим образом:



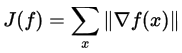
К сожалению, вычисление этого функционала нельзя сделать простым образом, поскольку здесь требуется применение весьма сложных техник оптимизации.

В качестве альтернативы можно использовать сглаженный функционал вместо абсолютного значения:



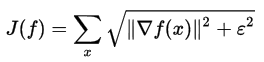
Когда эпсилон стремится к нулю, результат стремится к первоначальному определению Total Variation, но процесс оптимизации становится более сложным. И наоборот, при достаточном большом эпсилон результат оптимизации будет напоминать фильтр Винера с размытием краев. К сожалению, приведенная выше формула имеет неквадратичный вид, поэтому она не может быть просто вычислена в частотном пространстве Фурье, как это получалось с фильтрами Винера и Тихонова. Поэтому необходим один из методов пошаговой оптимизации для нахождения приближенного решения — например классический метод градиентного спуска:



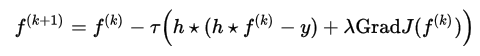
Где тау вычисляется по следующей формуле:



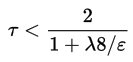
А градиент сглаженного функционала определяется как:



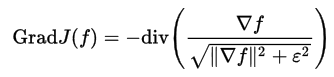
Количество итераций должно быть достаточно большим — несколько сотен.



Это самый базовый подход в реализации TV prior, что называется «в лоб». Тем не менее, даже он дает очень неплохие результаты. На базе его в научных публикациях появилось много исследований, которые пытаются еще улучшить качество, а также уменьшить время расчета.

Практическая реализация

Описанные формулы, в принципе, несложные, хотя и очень громоздкие в реализации. Основная проблема — достичь высокого быстродействия, т.к. количество итераций очень большое и каждая итерация содержит много сложных действий. А именно — несколько сверток изображения целиком, вычисления полного градиента и дивергенции.

Скажу сразу, добиться хорошей скорости работы мне пока не удалось, на изображении размером несколько мегапикселей время финального вычисления составляет 2-3 минуты. Но Preview работает быстро — порядка 0.2 секунды.

Сборку под Windows можно скачать по адресу:

github.com/downloads/Y-Vladimir/SmartDeblur/SmartDeblur-1.27-win.zip

Исходники (под лицензией GPL v3) доступны по ссылке: github.com/Y-Vladimir/SmartDeblur



Основные изменения по сравнению с прошлой версией, которая была описана во второй части:

• Добавлены два метода деконволюции: TV prior и фильтрация по Тихонову


• Добавлена поддержка восстановления Гауссового размытия


• Улучшена скорость работы (примерно в 2.5 раза)


• Уменьшено потребление памяти (примерно в 1.5 раза)


• Максимальный размер обрабатываемого изображения по умолчанию 3000 (но можно менять в настройках)


• Добавлена секция настроек


• Добавлен Updates Checker


• Поддержка Drag&Drop


• Добавлен Help Screen с примером изображения и советами по настройке


• Исправлен баг с рябью в режиме preview

Язык C++ с использованием Qt.

Сравнение

Ну и теперь самое главное — на какое же качество можно рассчитывать при обработке размытых изображений. Будем сравнивать с топовым коммерческим аналогом Topaz InFocus. Остальные аналоги (типа FocusMagic) уже давно не поддерживаются или дают уж совсем неприемлемые результаты обработки. Итак поехали.

Сначала возьмем рекламный пример с сайта Topaz InFocus: www.topazlabs.com/infocus/_images/licenseplate_compare.jpg





Вот результат от Topaz InFocus:







А вот результат работы SmartDeblur при следующих параметрах:

Type: Motion Blur, Length: 10.1, Angle: -45, Smooth: 60%





Как видим, результаты очень схожие. И не так очевидно, что лучше. Topaz InFocus, судя по всему, тоже использует алгоритм, похожий на TV prior плюс пост-обработка в виде шарпинга краев. Надо заметить, что приведенное исходное смазанное изображение, с очень большой вероятностью, является синтетическим. Т.е. взято неискаженное изображение и применен фильтр Motion Blur. Это видно по практически идеальному восстановлению, а также по подозрительно целым параметрам искажения — угол 45 градусов и длина 10 пикселей.



Теперь возьмем реальное изображение, которое я вчера сфоткал на свой Canon 500D с ручным уводом фокуса:





Результат от Topaz InFocus при следующих параметрах:

Type: Out-of-Focus, Radius: 5.5, Suppress Artifacts: 0.34





Результат SmartDeblur при следующих параметрах:

Type: Out of Focus, Radius: 5.9, Smooth: 60%





Тут ничья, можно сказать. Параметры в каждой программе подбирались так, чтобы обеспечить наилучшее качество.



Еще один реальный пример снятый мною:





Результат SmartDeblur при следующих параметрах:

Type: Motion Blur, Length: 6.6, Angle: -37, Smooth: 53%

Выводы

Подошла к концу третья заключительная статья. Получилась она не особо большой, но, надеюсь, будет полезной. Как видим полученное качество обработки уже вполне приемлемо для реального применения. Основная проблема, которая остается — в местах, где есть светлые объекты, после обработки получается заметный эффект звона. Думаю, это связано с тем, что на светлых участках нарушается линейность отображения яркости пикселей, что дает неверную интерпретацию о его реальной яркости. Возможно, нужна логарифмическая предобработка яркости, либо еще что-то.



Еще раз напомню:

Сборку под Windows можно скачать по адресу:

github.com/downloads/Y-Vladimir/SmartDeblur/SmartDeblur-1.27-win.zip

Исходники (под лицензией GPL v3) доступны по ссылке: github.com/Y-Vladimir/SmartDeblur



И как обычно — буду очень рад замечаниям и предложениям по SmartDeblur!

Кто будет пробовать программу — учтите, что параметр качества Smooth в режиме превью и в режиме High-Quality ведет себя весьма по-разному. Поэтому финальный результат ползунка сглаживания можно оценить только после завершения просчета High-Quality.



P.S. Огромная просьба ко всем, кто мне пишет на почту. После публикации двух предыдущих статьей мне пришло (и продолжает приходить) большое количество писем с просьбой восстановить номера машин на кадрах с камер видеонаблюдения, когда весь номер занимает площадь несколько пикселей.

Я этим не занимаюсь! SmartDeblur этого тоже делать не умеет. Это задача совсем другого рода, а именно Super-Resolution, когда из нескольких изображений малого разрешения получается изображение высокого разрешения с новыми деталями, которых не было на исходных данных. Может быть когда-нибудь ей и займусь, но точно не в ближайшее время.

Blind Deconvolution — автоматическое восстановление смазанных изображений

Смазанные изображения — один из самых неприятных дефектов в фотографии, наравне с расфокусированными изображениями. Ранее я писал про алгоритмы деконволюции для восстановления смазанных и расфокусированных изображений. Эти, относительно простые, подходы позволяют восстановить исходное изображение, если известна точная траектория смаза (или форма пятна размытия).

В большинстве случаев траектория смаза предполагается прямой линией, параметры которой должен задавать сам пользователь — для этого требуется достаточно кропотливая работа по подбору ядра, кроме того, в реальных фотографиях траектория смаза далека от линии и представляет собой замысловатую кривую переменной плотности/яркости, форму которой крайне сложно подобрать вручную.





В последние несколько лет интенсивно развивается новое направлении в теории восстановления изображений — слепая обратная свертка (Blind Deconvolution). Появилось достаточно много работ по этой теме, и начинается активное коммерческое использование результатов.

Многие из вас помнят конференцию Adobe MAX 2011, на которой они как раз показали работу одного из алгоритмов Blind Deconvolution: Исправление смазанных фотографий в новой версии Photoshop

В этой статье я хочу подробнее рассказать — как же работает эта удивительная технология, а также показать практическую реализацию SmartDeblur, который теперь тоже имеет в своем распоряжении этот алгоритм.

Внимание, под катом много картинок!

Начало

Этот пост является продолжением серии моих постов «Восстановление расфокусированных и смазанных изображений»:

Часть 1. Теория — Восстановление расфокусированных и смазанных изображений

Часть 2. Практика — Восстановление расфокусированных и смазанных изображений

Часть 3. Повышаем качество — Восстановление расфокусированных и смазанных изображений

Рекомендуется прочитать хотя бы первую теоретическую часть, чтобы лучше понимать, что такое свертка, деконволюция, преобразование Фурье и прочие термины. Хоть я и обещал, что третья часть будет последней, но не смог удержаться и не рассказать про последние веяния в области восстановления изображений.

Я буду рассматривать Blind Decovolution на примере работы американского профессора Rob Fergus «Removing Camera Shake from a Single Photograph». Оригинал статьи можно найти на его страничке: http://cs.nyu.edu/~fergus/pmwiki/pmwiki.php

Это не самая новая работа, в последнее время появилось много других публикаций, которые демонстрируют лучшие результаты — но там используется совсем сложная математика ((для неподготовленного читателя) в ряде этапов, а основной принцип остается тем же. К тому же, работа Фергуса является своего рода «классикой», он одним из первых предложил принципиально новый подход, который позволил автоматически определять ядро смаза даже для очень сложных случаев.

Модель искажения

И так, приступим.

Возьмем фотоаппарат и сделаем смазанный снимок — благо для этого не требуется особенных усилий :)





Введем следующие обозначения:

B — наблюдаемое смазанное изображение

K — ядро размытия (траектория смаза), kernel

L — исходное неразмытое изображение (скрытое)

N — аддитивный шум



Тогда процесс смаза/искажения можно описать в виде следующего выражения



B = K*L+N



Где символ "*" это операция свертки, не путать с обычным умножением!

Что такое свертка, можно прочитать в первой части

В наглядном виде это можно представить следующим образом (опустив для простоты шумовую составляющую):





Так что же является наиболее сложным?

Представим себе простую аналогию — число 11 состоит из двух множителей. Каковы они?

Вариантов решения бесконечно:

11 = 1 x 11

11 = 2 x 5.5

11 = 3 x 3.667

и т.д.

Или, переходя к наглядному представлению:

Целевая функция

Чтобы получить конкретное решение нужно вводить ограничения, как-то описывать модель того, к чему мы стремимся.

Т.е. нужно больше информации. Одним из вариантов этого является задание целевой функции — это такая функция, значение которое тем выше (в простом случае), чем ближе получаемый результат к желаемому.
Исследования показали, что несмотря на то, что реальные изображения имеют большой разброс значений отдельных пикселей, градиенты этих значений имеют вид распределения с медленно убывающими границами (Heavy-tailed distribution). Такое распределение имеет пик в окрестности нуля и, в отличие от гауссового распределения, имеет значительно большие вероятности больших значений (вот такое масло масляное).
Это совпадает с интуитивным представлением, что на реальных изображениях в большинстве случаев присутствуют большие области более-менее постоянной яркости, которые заканчиваются объектами с резкими и средними перепадами яркости.

Вот пример гистограммы градиентов для резкого изображения:


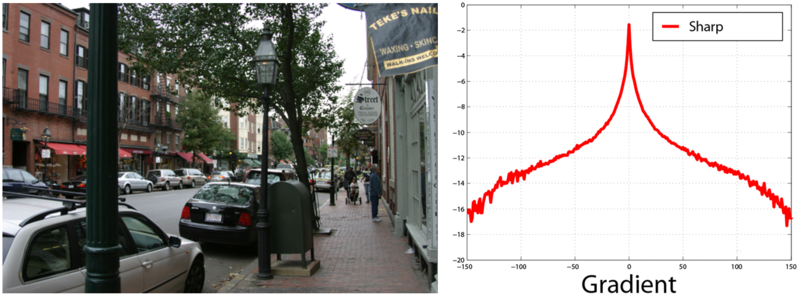
И для размытого изображения:


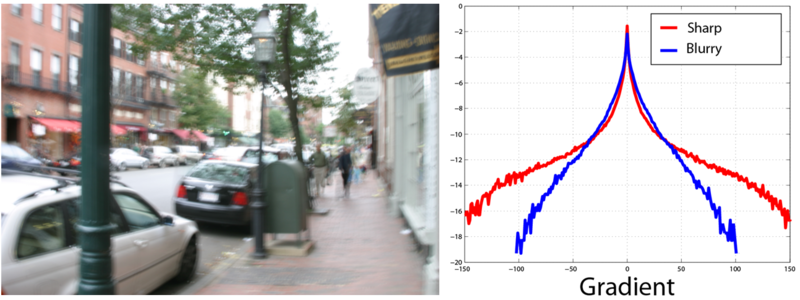
Таким образом мы получили инструмент, которые позволяет нам измерить «качество» получаемого результата с точки зрения четкости и похожести на реальное изображение.

Теперь мы можем сформулировать основные пункты для построение завершенной модели:
1. Ограничения накладываемые моделью искажения B = K*L+N
2. Целевая функция для результата реконструкции — насколько похожа гистограмма градиентов на теоретическое распределение с медленно убывающими границами. Обозначим ее как p(L_P)
3. Целевая функция для ядра искажения — положительные значения и низкая доля белых пикселей (т.к. траектория смаза обычно представлена тонкой линией). Обозначим ее как p(K)

Объединим все это в общую целевую функцию следующим образом:


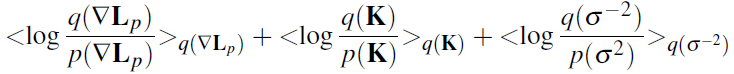
Где q(L_P), q(K) распределения, получаемые подходом Variational Bayesian

Далее эта целевая функция минимизируется методом покоординатного спуска с некоторыми дополнениями, которые я не буду описывать из-за их сложности и обилия формул — все это можно прочитать в работе Фергуса.
Этот подход позволяет улучшить качество имеющегося ядра, но им нельзя построить это ядро с нуля, т.к. скорее всего в процессе нахождения решения мы попадем в один из локальных минимумов.

Пирамидальный подход

Решением этой проблемы является итерационный подход к построению ядра искажения.
Вначале из входного размытого изображения мы строим пирамиду изображений с разным разрешением. От самого маленького размера до исходного размера.
Далее мы инициализируем алгоритм с помощью ядра размером 3*3 с одним из простых шаблонов — вертикальная линия, горизонтальная линия или гауссово пятно. В качестве универсального варианта можно выбрать последний — гауссово пятно.
Используя алгоритм оптимизации, описанный выше мы улучшаем оценку ядра, используя самый маленький размер изображения в построенной пирамиде.
После этого мы ресайзим полученное уточненное ядро до, скажем, 5*5 пикселей и повторяем процесс уже с изображением следующего размера.
Таким образом на каждом шаге мы чуть-чуть улучшаем ядро и в результате получаем весьма точную траекторию смаза.

Продемонстрируем итеративное построение ядра на примере.
Исходное изображение:


Процесс уточнения ядра:

Первая и третья строки показывают оценку ядра на каждом уровне пирамиды изображений.
Вторая и четвертая строки — оценка неискаженного изображения.

Результат:

Блок-схема алгоритма

Осталось собрать все вместе и описать алгоритм целиком:



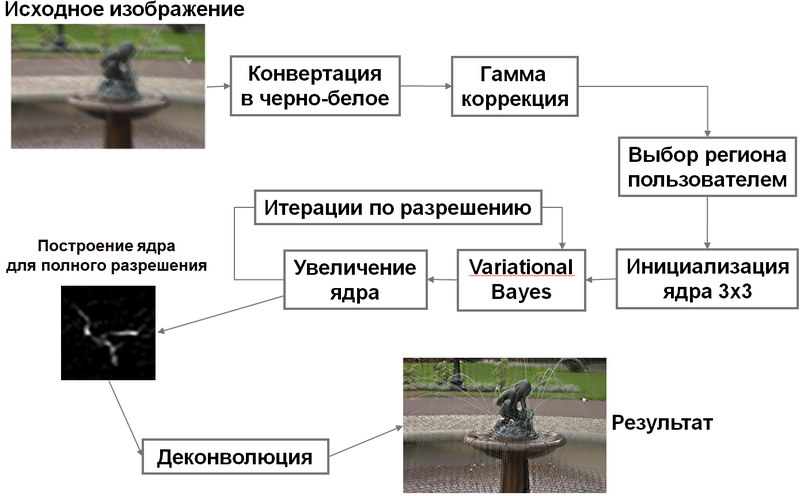
Более современные подходы имеют примерно такую идею последовательного уточнения ядра, но используют более изощренные варианты целевой функции для результата реконструкции и ядра искажения. Плюс к этому осуществляют промежуточную и финальную фильтрацию получаемого ядра, чтобы убрать лишний шум и исправить некоторые ошибки в алгоритме уточнения.

Практическая реализация

Наверное, самое интересное — это поиграться с алгоритмом Blind Deconvolution вживую на реальных изображениях!
Мы реализовали похожий вариант и добавили как новую функцию в SmartDeblur 2.0 — все по-прежнему бесплатно :)
Адрес проекта: smartdeblur.net/
(Исходники и бинарники от предыдущей версии можно найти на GitHub: github.com/Y-Vladimir/SmartDeblur )

Пример работы:


Другой пример:


И в заключение, результат работы на изображении c конференции Adobe MAX 2011:


Как видно, результат практически идеален — почти как у Adobe в их демонстрации.

Технические детали

Пока что максимальный размер обрабатываемого изображение установлен как 1200*1200. Это связано с тем, что алгоритмы потребляют очень много памяти. Даже на изображении 1000 пикселей — больше гигабайта. Поэтому введено ограничение на размер.
Позже увеличим его, после того как оптимизируем деконволюцию и пирамидальное построение.
Интерфейс выглядит следующим образом:



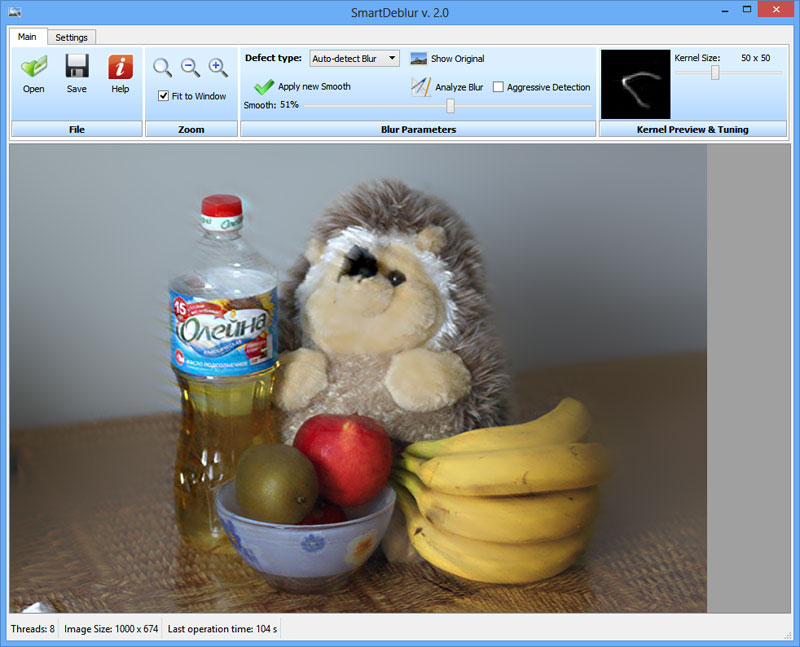
Для работы с программой требуется лишь загрузить изображение и нажать «Analyze Blur» и согласиться с выбором всего изображения — анализ может занят несколько минут. Если результат не устраивает, можно выбрать другой регион (выделить мышкой на изображении двигая ее вправо-вниз, немного не очевидно, но пока так :) ). Правой кнопкой выделение убирается.
Галочка «Agressive Detection» изменяет параметры, чтобы выделять только самые важные элементы ядра.

Пока что хорошие результаты достигаются далеко не на всех изображениях — поэтому будем очень рады фидбеку, это поможет нам улучшить алгоритмы!

Vladimir Yuzhikov (Владимир Южиков)

Источник:
http://habrahabr.ru/post/136853/
http://habrahabr.ru/post/147828/
http://habrahabr.ru/post/152885/